Apache Sling Context-Aware Configuration

About

These bundles provide a service API that can be used to get context-aware configurations. Context-aware configurations are configurations that are related to a content resource or a resource tree, e.g. a web site or a tenant site.

Here is an example how your content structure may look like:

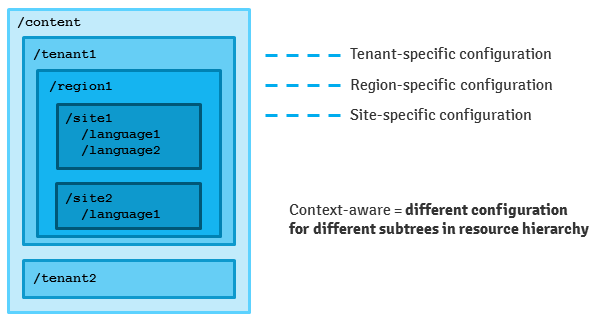
Configuration example

The application needs different configuration for different sites, regions and tenants = different contexts. Some parameters may be shared, so inheritance for nested contexts and from global fallback values is supported as well. You have full control which content subtrees are the contexts in your application, the structure above is only an example.

Using the Context-Aware Configuration Java API you can get the matching configuration for each content resource without caring where it is stored or how the inheritance works.

Java API

To get and use configurations, the Java API must be used. Any using code must not make any assumptions on how the context-aware configurations are searched or stored!

The Java API consists of two parts:

Context-Aware Resources: 'Low-level' API for accessing configuration resources (which can be anything, e.g. workflow definitions)
Context-Aware Configurations: 'High-level' API for accessing configuration data (key/value pairs)

In most cases you will use only the 'High-level' API for getting context-aware configurations.

Context-Aware Resources

The base concept are context-aware resources: for a given content resource, a named configuration resource can be get. The service for getting the configuration resources is called the ConfigurationResourceResolver. This service has two methods:

getting a named configuration resource
getting all child resources of a named configuration resource.

For example to get a configuration resource for a content resource at /content/mysite/page1, you would get a reference to the OSGi service org.apache.sling.caconfig.resource.ConfigurationResourceResolver and write:

Resource contentResource = resourceResolver.getResource("/content/mysite/page1");

Resource configResource = configurationResourceResolver.getResource(contentResource, "my-bucket", "my-config");

Or if you have several configuration resources of the same type and you need all of them:

Collection<Resource> configResources = configurationResourceResolver.getResourceCollection(contentResource, "my-bucket", "my-config");

The ConfigurationResourceResolver has a concept of "buckets" (2nd parameter in the method signatures) that allows to separate different types of configuration resources into different resource hierarchies, so you have a separate "namespaces" for the named configuration resources. For example one bucket for workflow definitions, one bucket for template definitions, one for key/value-pairs.

The configuration name (3rd parameter) defines which configuration you are interested in. The name can be a relative path as well (e.g. "sub1/my-config").

Context-Aware Configurations

While context-aware resources give you pure resources and your application code can decide what to do with it, the most common use case is some configuration. A configuration is usually described by an annotation class (like Declarative Services does for component configurations). These are typed configuration objects and the context-aware configuration support automatically converts resources into the wanted configuration type.

Context-aware configurations are built on top of context-aware resources. The same concept is used: configurations are named and the service to get them is the ConfigurationResolver. You can get a reference to the OSGi service org.apache.sling.caconfig.ConfigurationResolver - it has a single method to get a ConfigurationBuilder. Alternatively you can directly adapt your content resource directly to the ConfigurationBuilder interface and get the configuration:

Resource contentResource = resourceResolver.getResource("/content/mysite/page1");

MyConfig config = contentResource.adaptTo(ConfigurationBuilder.class).as(MyConfig.class);

Or if you want to get a list of configurations:

Collection<MyConfig> configs = contentResource.adaptTo(ConfigurationBuilder.class).asCollection(MyConfig.class);

The ConfigurationBuilder also supports getting the configurations as ValueMap or by adapting the configuration resources e.g. to a Sling Model. In this case you have to specify a configuration name which is otherwise derived automatically from the annotation class.

Internally the ConfigurationResolver used the ConfigurationResourceResolver to get the configuration resources. It uses always the bucket name sling:configs.

Contexts and configuration references

When you use the Default Implementation contexts in the content resource hierarchy is defined by setting sling:configRef properties. Each resource that has a sling:configRef property set defines the root resource of a context, the whole subtree is the context. Within the subtree further nested contexts can be defined. The property contains a resource path pointing to a resource below /conf. This is the configuration reference.

Example:

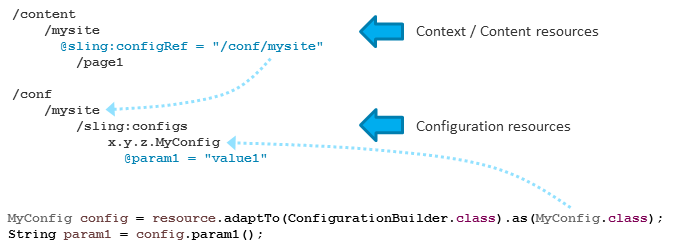
Context and config reference

If you define nested contexts or use a deeper hierarchy of resourced in /conf the inheritance rules are applied. Additionally it is possible to define default values as fallback if no configuration resource exists yet in /conf. See Default Implementation for details.

Describe configurations via annotation classes

You need an annotation class for each configuration you want to read via the ConfigurationBuilder. The annotation classes may be provided by the applications/libraries you use, or you can define your own annotation classes for your application.

The annotation class may look like this:

@Configuration(label="My Configuration", description="Describe me")
public @interface MyConfig {
  	
    @Property(label="Parameter #1", description="Describe me")
    String param1();
    
    @Property(label="Parameter with Default value", description="Describe me")
    String paramWithDefault() default "defValue";
    
    @Property(label="Integer parameter", description="Describe me")
    int intParam();
}

The @Configuration annotation is mandatory. All properties on the @Configuration annotation and the @Property annotations are optional - they provide additional metadata for tooling e.g. configuration editors.

By default the annotation class name is used as configuration name, which is also the recommended option. If you want to use an arbitrary configuration name you can specify it via a name property on the @Configuration annotation.

You may specify custom properties (via property string array) for the configuration class or each properties. They are not used by the Sling Context-Aware configuration implementation, but may be used by additional tooling to manage the configurations.

If you provide your own configuration annotation classes in your bundle, you have to export them and list all class names in a bundle header named Sling-ContextAware-Configuration-Classes - example:

Sling-ContextAware-Configuration-Classes: x.y.z.MyConfig, x.y.z.MyConfig2

To automate this you can use the Context-Aware Configuration bnd plugin (see next chapter).

Accessing configuration from HTL/Sightly templates

Context-Aware configuration contains a Scripting Binding Values provider with automatically registeres a caconfig variable in your HTL/Sightly scripts to directly access context-aware configurations. It supports both singleton configurations and configuration lists. Please note that configuration lists are only supported when configuration metadata is present (e.g. via an annotation class).

Example for accessing a property of a singleton configuration (with a config name x.y.z.ConfigSample):

<dl>
    <dt>stringParam:</dt>
    <dd>${caconfig['x.y.z.ConfigSample'].stringParam}</dd>
</dl>

Example for accessing a property of a configuration list (with a config name x.y.z.ConfigSampleList):

<ul data-sly-list.item="${caconfig['x.y.z.ConfigSampleList']}">
    <li>stringParam: ${item.stringParam}</li>
</ul>

If you want to access nested configurations, you have to use a slash "/" as a separator in the config name. Example:

${caconfig['x.y.z.ConfigSample/nestedConfig'].stringParam}

Context-Aware Configuration bnd plugin

A bnd plugin is provided that scans the classpath of a bundle Maven project at build time and automatically generates a Sling-ContextAware-Configuration-Classes bundle header for all annotation classes annotated with @Configuration. It can be used by both maven-bundle-plugin and bnd-maven-plugin, as both use the bnd library internally.

Example configuration:

<plugin>
    <groupId>org.apache.felix</groupId>
    <artifactId>maven-bundle-plugin</artifactId>
    <extensions>true</extensions>
    <configuration>
        <instructions>
            <!-- Generate bundle header containing all configuration annotation classes -->
            <_plugin>org.apache.sling.caconfig.bndplugin.ConfigurationClassScannerPlugin</_plugin>
        </instructions>
    </configuration>
    <dependencies>
        <dependency>
            <groupId>org.apache.sling</groupId>
            <artifactId>org.apache.sling.caconfig.bnd-plugin</artifactId>
            <version>1.0.2</version>
        </dependency>
    </dependencies>
</plugin>

If you use the bnd-maven-plugin and raw bnd statements, you have to configure it with this bnd statement:

<plugin>
    <groupId>biz.aQute.bnd</groupId>
    <artifactId>bnd-maven-plugin</artifactId>
    <configuration>
    	<bnd><![CDATA[
            ...
        	-plugin org.apache.sling.caconfig.bndplugin.ConfigurationClassScannerPlugin
    	]]></bnd>
    </configuration>
    <dependencies>
        <dependency>
            <groupId>org.apache.sling</groupId>
            <artifactId>org.apache.sling.caconfig.bnd-plugin</artifactId>
            <version>1.0.2</version>
        </dependency>
    </dependencies>
</plugin>

Unit Tests with Context-Aware Configuration

When your code depends on Sling Context-Aware Configuration and you want to write Sling Mocks-based unit tests running against the Context-Aware configuration implementation you have to register the proper OSGi services to use them. To make this easier, a "Apache Sling Context-Aware Configuration Mock Plugin" is provided which does this job for you.

Example for setting up the unit test context rule:

import static org.apache.sling.testing.mock.caconfig.ContextPlugins.CACONFIG;

public class MyTest {

	@Rule
	public SlingContext context = new SlingContextBuilder().plugin(CACONFIG).build();

	@Before
	public void setUp() {
		// register configuration annotation class
		MockContextAwareConfig.registerAnnotationClasses(context, SimpleConfig.class);
	}
...

In you project define a test dependency (additionally the sling-mock dependency is required):

<dependency>
  <groupId>org.apache.sling</groupId>
  <artifactId>org.apache.sling.testing.caconfig-mock-plugin</artifactId>
  <scope>test</scope>
</dependency>

Full example: Apache Sling Context-Aware Configuration Mock Plugin Test

Customizing the configuration lookup

The Context-Aware Configuration implementation provides a set of Service Provider Interfaces (SPI) that allows you to overlay, enhance or replace the default implementation and adapt it to your needs.

See SPI for details.

You can also override specific context-aware configuration within an instance - see Override for details.

Web Console plugins

The Context-Aware Configuration implementation provides two extension to the Felix Web Console:

A plugin "Sling / Context-Aware Configuration" that allows to test configuration resolution and prints outs all metadata. This is helpful debugging the resolution and collection and property inheritance. For each resource and property value the the real source resource path is listed.
A inventory printer "Sling Context-Aware Configuration" which lists all SPI implementations that are deployed, and additionally prints out all configuration metadata and override strings

To use the web console plugin you need to configure a "Service User" mapping for the bundle org.apache.sling.caconfig.impl to a system user which has read access to all context and configuration resources. By default this should be /content, /conf, /apps/conf and /libs/conf.

Management API

The Context-Aware Configuration Implementation Bundle provides a Management API which allows to read and write configuration data. It supports only Context-Aware configurations, not context-aware resources. It should not be used directly in applications, but is intended to provide an API for editor GUIs and other tools which allow to manage configurations.

The main entry point is the OSGi service org.apache.sling.caconfig.management.ConfigurationManager. It allows to get, write or delete singleton configurations and configuration lists. Configuration data is returned using ConfigurationData and ConfigurationCollectionData objects which also provide access to additional metadata about the resolving process and inheritance/override status of each property. Internally the configuration manager uses the SPI implementation to resolve and write the configuration data.

Whenever configuration data is read or written from the configuration resources a filtering of property names is applied to make sure "system properties" like jcr:primaryType or jcr:created are not returned as part of the configuration data. A list of regular expressions for this filtering can be configured via the "Apache Sling Context-Aware Configuration Management Settings" OSGi configuration. The configuration is accessible to custom persistence implementations via the org.apache.sling.caconfig.management.ConfigurationManagementSettings OSGi service. By default all properties in the jcr: namespace are filtered out.